My introduction to APL consisted of using the language to solve a number of quick puzzles; the phase 1 problems from Dyalog's annual Student Competition. It was a fantastic way to get to grips with each of the glyphs and the capabilities of the language.
While the puzzles were a far cry from real life problems, and the solutions a far cry from production code, the value in puzzling comes from the principles expounded in them.
Puzzling with purpose
Taking an example from the 2019 Phase 1 problems; generating the list of Knight moves given its starting position on a Chess board. If the knight starts on f3, it can move to 8 new squares: d2, d4, e1, e5, g1, g5, h2, and h4. If it starts on a7 though, it can only move to 3 new squares: b5, c6, and c8.
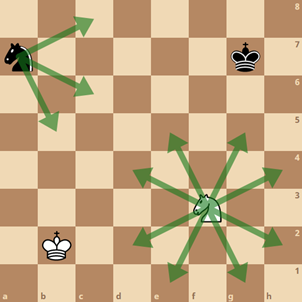
While quite a simple task, it highlights the array-oriented approach that APL excels at, and is a perfect introduction to some common glyphs and functions;
- The outer product can be used to generate the board co-ordinates, and potential moves.
- The transpose, rotate, and reverse functions can be used to orient the board the correct way (though this isn’t actually required for the solution, the chess player in me makes this necessary).
- Removing impossible or illegal moves can introduce how Boolean logic can operate over an array.
While it’s very unlikely that a client or customer is going to approach us and say “Quick! We need to calculate the number of possible knight moves from a given location, stat!” it’s very likely that a future task will require altering the structure of some data using some of the principles practiced here.
What is a Quine?
The name "quine" was coined by Douglas Hofstadter, in one of my favourite books Gödel, Escher, Bach: An Eternal Golden Braid, after the philosopher Willard Van Orman Quine, who made an extensive study of indirect self-reference. In programming, a program is called a quine if the output when run is an exact copy of the program, i.e. a program that prints itself! Quines have been written for an enormous number of languages, ranging from a few characters (or even 0 in the case of the empty program quine) to being possible in theory, but too large to even fit in the known universe. It is theoretically possible to write a quine for any Turning-complete language with the capability to output any computable string, due to Kleene's recursion theorem.
Quining with purpose?
Are they actually useful? Probably not! But similar to the example above, the value comes not from the solution directly, but from the practice of examining the language, how your program with be interpreted, and what the expected output should be, helping you to better understand the tool you are working with. The tricks and tactics employed by programmers writing quines are fascinating, and some of the best examples can be found in this Stack Exchange post.
A quine in APL
In typical APL fashion, the quines I have found for this language are incredibly concise, the shortest of which is only 18 characters;
1⌽,⍨9⍴'''1⌽,⍨9⍴'''
A brief dissection of how this quine works:
- The code wrapped in triple quotes
'''1⌽,⍨9⍴'''when executed by itself gives us '1⌽,⍨9⍴' - This character vector is scalar extended by the dyadic use of ⍴ function to 9 characters long, giving us
'1⌽,⍨9⍴'' - The commuted catenate,
⍨(sometimes called a selfie) causes the string to be catenated to itself, now outputting'1⌽,⍨9⍴'''1⌽,⍨9⍴'' - The dyadic use of
1⌽rotates the character vector by 1 position, placing the single quote from the beginning at the end, reproducing our program!
How quinetessentially APL!
APL Developer
Jonners is an APL Developer. Born and raised in Horsham. He studied all things scientific at college, and went on to study Physics at university. After a brief soujourn studying guitar making and repair for a couple of years, he got his first job in software in the QA department, working on automated testing systems, picking up a bit of Python and SQL as he went. Having discovered APL through a friend, he started using it to solve puzzles, and joined Optima soon after.

