My first hobby code project in APL was signal processing tools. It was something I had studied in university and felt like a good candidate for APL programming. When I saw a question about sound in APL in the Dyalog forum recently, it rekindled my interest and I decided to explore the domain again, 10 years later.

The question posed by Stuart Smith in the forum was how to play audio from APL, specifically a vector of samples rather than an external audio file. As you can read in the forum, Ray Cannon offered a few snippets to a Windows PlaySound function that plays back wave files. My contribution was to refactor the code and provide instructions on how to play wave streams from memory rather than file. You can find the code on GitHub under the project name apl-sound-wave.

With the tools to play wave streams ready, the next question is how to generate them.

Making waves

Sound waves in the physical world are basically propagating shifts in pressure. In electronic systems, sounds are generated by moving a membrane back and forth, thereby compressing and decompressing the air in the near vicinity of the membrane. In computers we can describe the movement of the membrane as a series of positions in either direction of a central resting point. A value of 0 is the resting point, +1 is far out and -1 far in. Given this we could make the membrane move back and forth by sending alternating numbers of +1 and -1. That is a very crude description of how sound is generated, but it forms the basics for what we will look at now.

The most basic sound wave that occurs in nature is a sinusoid wave. This is a smooth, continuous, oscillating wave. So how do you generate that from a digital computer? The short answer is: by approximation. The digital version of an analog wave is a series of samples taken on a regular basis. This is referred to as the sample rate with the unit Hz and denotes the number of samples taken per second.

In APL we can use the circular functions to generate sample values for a sinusoid wave. The sine function has a period of 2π, so if we want to look at a single cycle we need to generate values that are in the range of [0,2π]. In APL the sine function is generated using the dyadic circle 1○ and π is generated using the monadic circle 2π = ○2.

To generate 4 samples of the sine wave we write:

      1○○2×(⍳4)÷4
1 1.224646799E¯16 ¯1 ¯2.449293598E¯16

We see that the 4 samples are essentially 1 0 -1 0, not very smooth. Let’s take a few more samples and chart the result:

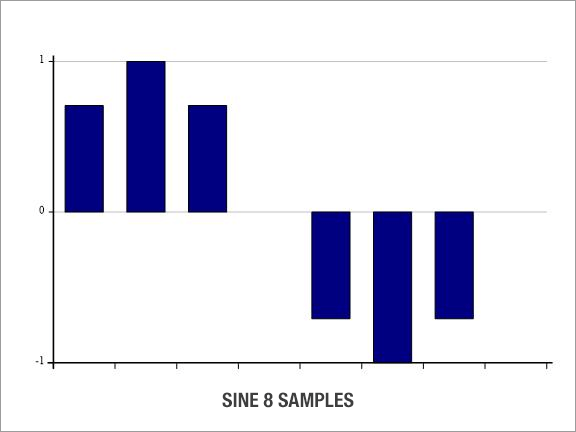
      sine←1○○2×(⍳8)÷8
      ]chart sine

Note: If you are on D15.0 and get a DOMAIN ERROR when you run the ]chart user command you may need to run ]uupdate first as there is a known bug in the user command. If that doesn’t help, edit the GetDyalogPath function in the DyalogInstallationFolderSALTspicechartwizard.dyalog script and make sure it appends a backslash to the path.

Try increasing the number a few times and look at the result.

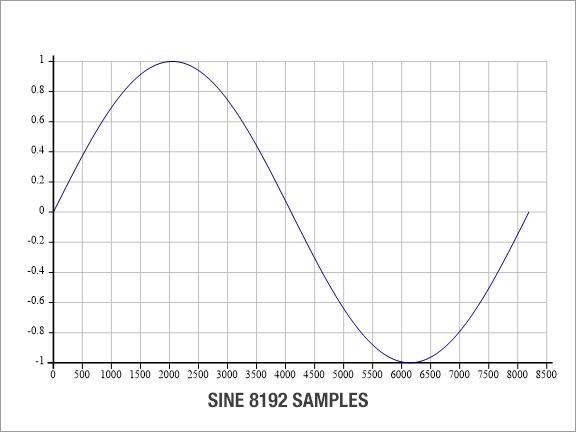
In our above example we effectively generated a sine wave with a frequency of 1Hz (one complete cycle per second). To increase the frequency of the wave we need to amend our formula above. This is done by simply multiplying the argument of the sine function with the chosen frequency:

sine←1○○2×freq×(⍳Fs)÷Fs

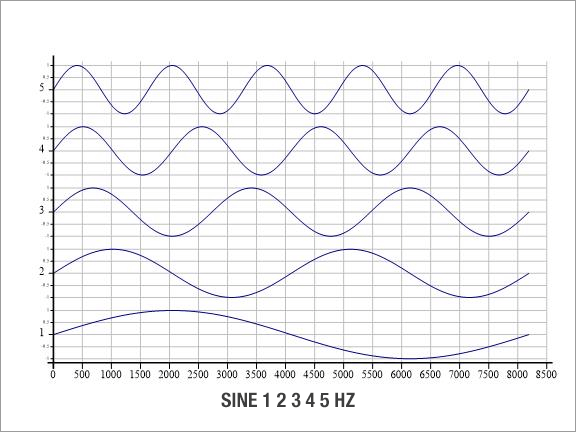
Where freq is the chosen frequency and Fs the sample rate. Lets look at a few different frequencies:

      s1←1○○2×1×(⍳8192)÷8192
      s2←1○○2×2×(⍳8192)÷8192
      s3←1○○2×3×(⍳8192)÷8192
      s4←1○○2×4×(⍳8192)÷8192
      s5←1○○2×5×(⍳8192)÷8192
      ]chart s1 s2 s3 s4 s5

Feel free to explore the ChartWizard and change styles to get a better view of the data. Try clicking the chart button as indicated below:

In the new window that appears, select a different style for your chart, for example select the Trace chart to see the waves stacked above each other.

To generate a musical note A we need to produce a wave with a frequency of 440Hz. If we choose a sample rate of 8192Hz for our generated digital wave and we want a duration of 5 seconds, it means we need to generate 5 x 8192 sample values. How do we define the duration of the generated wave? So far they have all lasted for one second. To alter the duration we just need to extend the indices created by the factor desired and also round it to whole integers:

sine←1○○2×freq×(⍳⌈dur×Fs)÷Fs

And we end up with the expression:

noteA←1○○2×440×(⍳⌈5×8192)÷8192

Which we can play by calling:

#.Sound.{SND_MEMORY PlaySound Wave ⍵}⍪noteA